What is a Fractional Integral?

It was shown a previous post how to define and calculate a function’s $\alpha$-th fractional integral, where $\alpha$ is a non-negative real number. Using this technique one can also define a function’s $\alpha$-th primitive. Now one will be able to see what such a primitive actually looks like through three examples.

Recall that the $\alpha$-th primitive of $f_0$ is defined as $$ f_{\alpha}(x) := \frac{1}{\Gamma(\alpha)} \int_0^{x} (x - s)^{\alpha-1} f_0(s) ds. $$

Code

The following examples come from a notebook where the fractional integral is implemented. It as available on github. An interactive notebook can be found and also a python script where a all the calculations implemented in another file are executed.

Examples

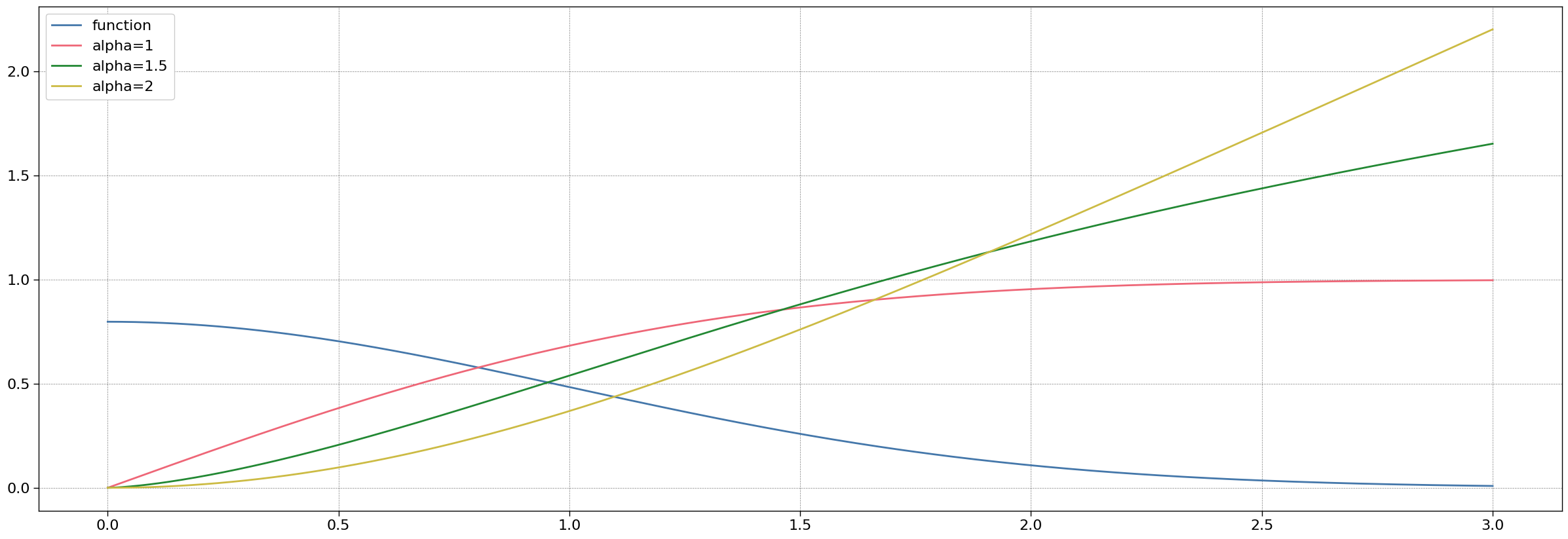
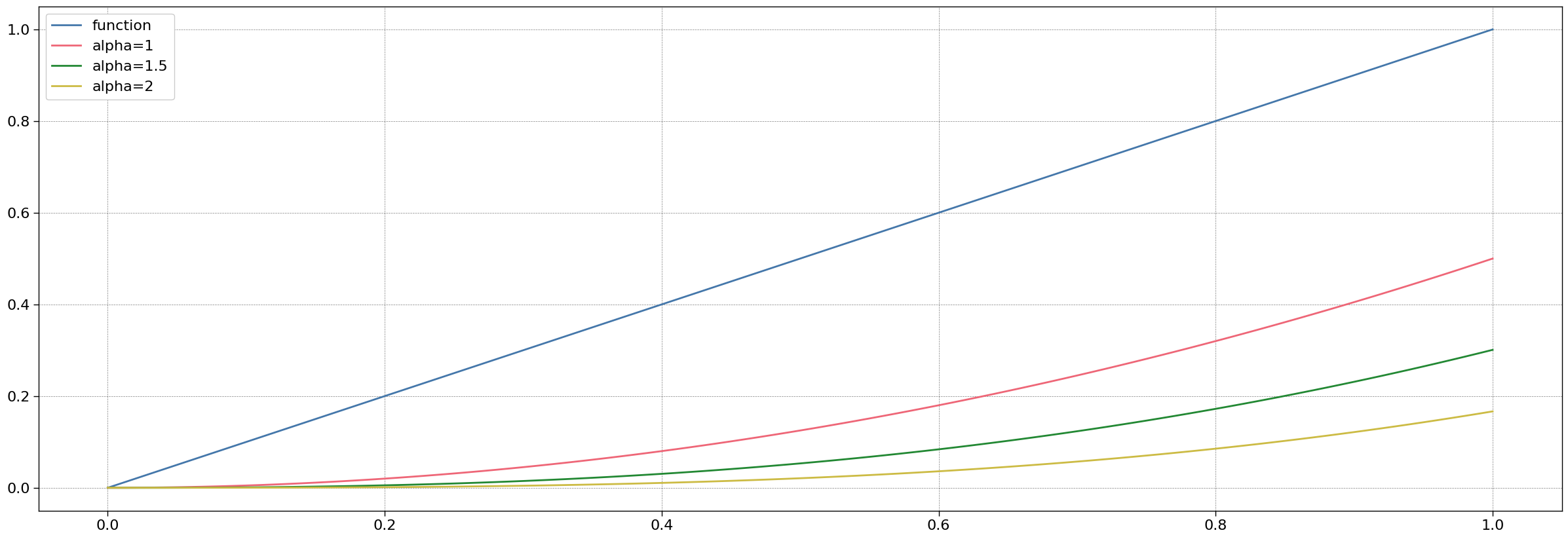
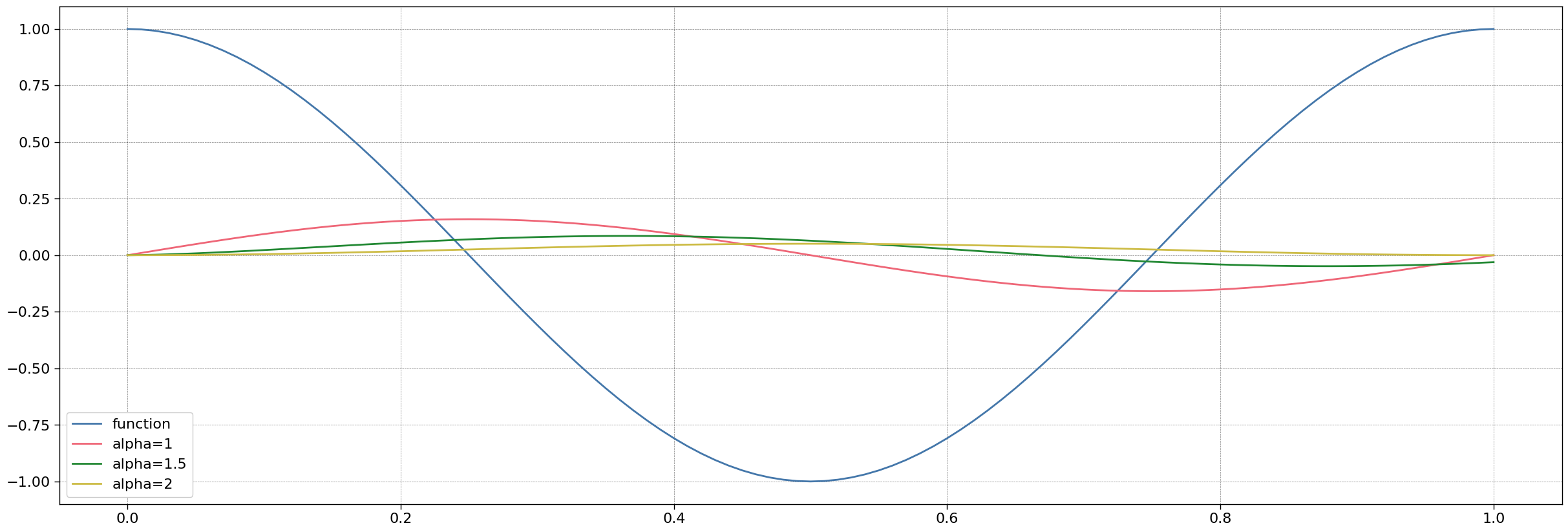
All the examples calculate the primitive of order $\alpha=1$, $\alpha=1.5$ and $\alpha=2$.

First Example

In this example one defines $f(x) := x$. This is the simplest case.

Second Example

In this example one integrates a trigonometric function $g(x) := \cos(2\pi x)$.

Third Example

Finally one considers a probability distribution $h(x) := \sqrt{\frac{2}{\pi}} \exp{ \Big( \frac{-x^2}{2} \Big)}$. This is the probability density function of a truncated gaussian on $[0,\infty)$.